I don't post much about the actual math that we do in class, but I gave my precalc kids an assignment yesterday that showed this (what I thought was) cool pattern in cubic functions.
It started with a function.
f(x) =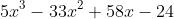
Their paper showed a graph and asked to find the zeros. We picked out 2 and 4 (checked with synthetic division) and ended up with 3/5 as our last.
Then it went through a process to build the cubic polynomial if you know the zeros (without doing all of the messy binomial multiplication).
Step 1: Factor out the 5. (This only works if the leading coefficient of 1).
=5(x^{3}-\frac{33}{5}x^{2}+\frac{58}{5}x-\frac{24}{5}) "f(x)=5(x^{3}-\frac{33}{5}x^{2}+\frac{58}{5}x-\frac{24}{5})")
Step 2. Find the product of the zeros.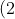(4)\left ( \frac{3}5{} \right )=\frac{24}{5} "(2)(4)\left ( \frac{3}5{} \right )=\frac{24}{5}")
(Which is the opposite of the constant term.)
Step 3. Find the sum of the zeros.
(Which is the opposite of the quadratic term.)
Step 4. Find the sum of the pairwise products (this totally confused most of the kids... ) which is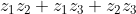
.
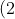(4)+(2)(\frac{5}{3})+(4)(\frac{5}{3})=\frac{58}{5} "(2)(4)+(2)(\frac{5}{3})+(4)(\frac{5}{3})=\frac{58}{5}")
(Which is the same as the linear term.)
So if you have the zeros of a cubic polynomial with leading coefficient of 1, you can use these patterns to find the polynomial itself. I thought that was pretty cool (and I found a couple of kids that agreed with me. The others not so much.).
The next problem was to find a cubic polynomial with zeros at 5,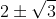
. (It ends up being f(x) = 
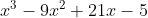if you're playing along at home. :)
Oh, and a couple of other things happened today:
1. Got a new girl in my honors precalc 1st period class. She just moved in from a school on the other side of the city. She "didn't have a clue" as to what we were doing and had been solving linear systems in her old school. I gave her a copy of the summer work that the precalc kids had done for her to look through; she asked if there were notes somewhere that she could use because she didn't remember any of it. Oh my. I actually emailed a friend who happens to teach at the girl's old school to do some checking; she said she should be fine (is just kind of "flaky") and was going to check with the Honors Alg2 teacher to see what they'd been doing.
2. Had my first "I'm overwhelmed" crier in another precalc class. This student had been absent for a couple of days and hasn't made any effort (that I've seen) to make things up. She told me when looking at their review for tomorrow's quiz that she didn't know any of it. I told her to come after school and we'd work through some problems; hopefully she'll have calmed down enough to realize that she does know it and was just stressed out.
f(x) =
Their paper showed a graph and asked to find the zeros. We picked out 2 and 4 (checked with synthetic division) and ended up with 3/5 as our last.
Then it went through a process to build the cubic polynomial if you know the zeros (without doing all of the messy binomial multiplication).
Step 1: Factor out the 5. (This only works if the leading coefficient of 1).
Step 2. Find the product of the zeros.
(Which is the opposite of the constant term.)
Step 3. Find the sum of the zeros.
(Which is the opposite of the quadratic term.)
Step 4. Find the sum of the pairwise products (this totally confused most of the kids... ) which is
So if you have the zeros of a cubic polynomial with leading coefficient of 1, you can use these patterns to find the polynomial itself. I thought that was pretty cool (and I found a couple of kids that agreed with me. The others not so much.).
The next problem was to find a cubic polynomial with zeros at 5,
Oh, and a couple of other things happened today:
1. Got a new girl in my honors precalc 1st period class. She just moved in from a school on the other side of the city. She "didn't have a clue" as to what we were doing and had been solving linear systems in her old school. I gave her a copy of the summer work that the precalc kids had done for her to look through; she asked if there were notes somewhere that she could use because she didn't remember any of it. Oh my. I actually emailed a friend who happens to teach at the girl's old school to do some checking; she said she should be fine (is just kind of "flaky") and was going to check with the Honors Alg2 teacher to see what they'd been doing.
2. Had my first "I'm overwhelmed" crier in another precalc class. This student had been absent for a couple of days and hasn't made any effort (that I've seen) to make things up. She told me when looking at their review for tomorrow's quiz that she didn't know any of it. I told her to come after school and we'd work through some problems; hopefully she'll have calmed down enough to realize that she does know it and was just stressed out.
Comments
Post a Comment